You're reading the documentation of the v0.11. For the latest released version, please have a look at v0.12.

Graph States generation and display

This notebook need the python modules qiskit, qutip and seaborn to be able to run. Simply run :

pip install qiskit qutip seaborn

Some definitions and properties of graph states

Graph states are specific entangled states that are represented by a graph. They have interesting properties in many fields of quantum computing [1], therefore they are points of interest.

Definition:

Two definitions of a graph state exist. Since they are equivalent, we will only consider the following:

Given a graph \(G=(V,E)\), with the set of vertices \(V\) and the set of edges \(E\), the corresponding graph state is defined as:

\(\left|G\right\rangle = \prod_{(a,b)\in E} CZ^{\{a,b\}} \left|+\right\rangle^{\otimes V}\)

where \(|+\rangle = \frac{|0\rangle + |1\rangle}{\sqrt2}\) and \(CZ^{\{a,b\}}\) is the controlled-Z interaction between the two vertices (corresponding to two qubits) \(a\) and \(b\). The operators order in the product doesn’t matter since CZ gates commute between themselves. We can write the CZ gate with the following matrix :

\(CZ = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{bmatrix}\)

Therefore, we can write the action of a CZ gate as: \(CZ^{\{1,2\}}|0\rangle_1 |\pm\rangle_2 = |0\rangle_1 |\pm\rangle_2\) and \(CZ^{\{1,2\}}|1\rangle_1 |\pm\rangle_2 = |1\rangle_1 |\mp\rangle_2\).

Let’s illustrate this with an example. The associated graph of: \(|\Psi_{graph}\rangle = CZ^{\{0,1\}}\, CZ^{\{1,2\}}\, CZ^{\{0,2\}}\, CZ^{\{3,2\}}|+\rangle_0 |+\rangle_1 |+\rangle_2 |+\rangle_3\) is the following. The graph is generated as an output later in this notebook. We will now see several ways to create and display these states.

Generating entangled states with a circuit

We will first use a 3-qubits circuit. We need to implement two CZ gates on it to generate the 3-qubits linear graph state.

These gates are post-selected CZ gates which have a probability of success of \(\frac{1}{9}\).

import math

import perceval as pcvl

from perceval.utils import StateGenerator, Encoding
from perceval.converters import StatevectorConverter

import networkx as nx

from qiskit.visualization import plot_state_qsphere

from qutip import plot_schmidt

For this circuit, we use path encoded qubits with 3 photons as input.

# Modes number of the circuit
m = 10

def cz(i):
    """Return a post selected CZ gate labeled with i"""

    CZ = pcvl.Circuit(6, name="CZ" + str(i))
    CZ.add((0, 1), pcvl.BS(pcvl.BS.r_to_theta(1/3)))
    CZ.add((2, 3), pcvl.BS(pcvl.BS.r_to_theta(1/3)))
    CZ.add((4, 5), pcvl.BS(pcvl.BS.r_to_theta(1/3)))
    CZ.add(2, pcvl.PS(math.pi))

    return CZ

# Creation of the full circuit
c_graph_lin = pcvl.Circuit(10, name="C_Graph")\
    .add((1, 2), pcvl.BS()).add(1, pcvl.PS(math.pi/2))\
    .add((3, 4), pcvl.BS()).add(3, pcvl.PS(math.pi/2))\
    .add((7, 8), pcvl.BS()).add(7, pcvl.PS(math.pi/2))\
    .add(0, cz(1), merge=False)\
    .add((3,4,5,6), pcvl.PERM([2, 3, 0, 1]))\
    .add(4, cz(2), merge=False)\
    .add(8, pcvl.PS(math.pi/2)).add(7, pcvl.PS(math.pi/2))\
    .add((3,4,5,6), pcvl.PERM([2, 3, 0, 1]))

pcvl.pdisplay(c_graph_lin, recursive=True, render_size=0.6)

Logical states are path encoded on the Fock States.

Due to post-selection, only few states of the full Fock space are relevant.

• Mode 0,5,6,9 are auxiliary.

• 1st qubit is path encoded in modes 1 & 2

• 2nd qubit in 3 & 4

• 3rd qubit in 7 & 8

# Basis for three qubits
states = [
    pcvl.BasicState([0,1,0,1,0,0,0,1,0,0]),  #|000>
    pcvl.BasicState([0,1,0,1,0,0,0,0,1,0]),  #|001>
    pcvl.BasicState([0,1,0,0,1,0,0,1,0,0]),  #|010>
    pcvl.BasicState([0,1,0,0,1,0,0,0,1,0]),  #|011>
    pcvl.BasicState([0,0,1,1,0,0,0,1,0,0]),  #|100>
    pcvl.BasicState([0,0,1,1,0,0,0,0,1,0]),  #|101>
    pcvl.BasicState([0,0,1,0,1,0,0,1,0,0]),  #|110>
    pcvl.BasicState([0,0,1,0,1,0,0,0,1,0])   #|111>
]

We will then simulate this circuit using the SLOS backend and compute the amplitudes for the output state.

# Simulator
backend = pcvl.BackendFactory.get_backend("SLOS")
backend.set_circuit(c_graph_lin)

We use the state \(|000\rangle\) as input state.

# Input state
input_state = pcvl.BasicState([0,1,0,1,0,0,0,1,0,0])
backend.set_input_state(input_state)

# Output state
output_state = pcvl.StateVector()
for state in states:
    ampli = backend.prob_amplitude(state)
    output_state += ampli*pcvl.StateVector(state)

print("The output state is :", output_state)

The output state is : sqrt(2)/4*|0,0,1,0,1,0,0,0,1,0>+sqrt(2)/4*|0,0,1,1,0,0,0,1,0,0>-sqrt(2)/4*|0,1,0,0,1,0,0,0,1,0>+sqrt(2)/4*|0,1,0,0,1,0,0,1,0,0>+sqrt(2)/4*|0,1,0,1,0,0,0,0,1,0>-sqrt(2)/4*|0,0,1,0,1,0,0,1,0,0>+sqrt(2)/4*|0,0,1,1,0,0,0,0,1,0>+sqrt(2)/4*|0,1,0,1,0,0,0,1,0,0>

As wanted, we obtain the linear graph states for three qubits which is : \(\frac{1}{\sqrt 8} (|000\rangle + |001\rangle + |010\rangle - |011\rangle + |100\rangle + |101\rangle - |110\rangle + |111\rangle )\).

This state is also locally equivalent to a \(GHZ\) state and we can therefore obtain it by performing local unitary single qubit transformations.

Representing a multi-qubit state

To represent the state we obtained, we use plot_state_qsphere from Qiskit [2] .

In order to do so we propose a converter to make a StateVector from Perceval compatible with a Statevector from Qiskit that can be interpreted by qsphere. It is important to consider that Qiskit only implements Statevectors that represent n-qubits states. A state in dual rail encoding like \(|0,1,0,1,0,0,0,1,0,0 \rangle\) from Perceval can’t be directly interpreted by it.

Therefore, the type of encoding (RAW, DUAL_RAIL, POLARIZATION…) needs to be given to the converter and the optional parameter anscillae corresponds to the list of modes that we don’t consider in the multi-qubits state. In our example these modes are the auxiliary modes 0,5,6 and 9.

We create the converter with the desired parameters:

converter = StatevectorConverter(encoding=Encoding.DUAL_RAIL, ancillae=[0,5,6,9])

We can then used it to convert any vector from Perceval to Qiskit.

qiskit_sv = converter.to_qiskit(output_state)

And represent it with qsphere.

Each small sphere represents one component of the superposition of states. Its size represents the modulus of the amplitude and its color represents the phase. For this representation, qsphere always fixes the global phase to 0.

plot_state_qsphere(qiskit_sv)

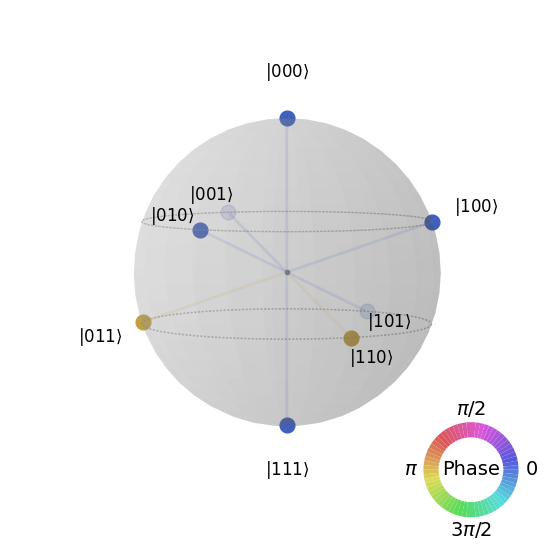
After defining a converter, it is also possible to do the conversion the other way around using : pcvl_sv = converter.to_perceval(qiskit_sv).

We also propose a conversion to qutip with the same converter : qutip_sv = converter.to_qutip(pcvl_sv).

The command to_perceval is both compatible with Qiskit and qutip.

For instance, we can represent a Bell state \(|\Psi^->\) in polarization encoding from Perceval with the function plot_schmidt from qutip [3] :

# Bell state in Perceval
generator = StateGenerator(Encoding.POLARIZATION)
pcvl_bell = generator.bell_state("psi-")
print(pcvl_bell)

# pcvl_bell = pcvl.StateVector('|{P:H},{P:V}>') - pcvl.StateVector('|{P:V},{P:H}>')

-sqrt(2)/2*|{P:V},{P:H}>+sqrt(2)/2*|{P:H},{P:V}>

# Conversion
converter = StatevectorConverter(encoding=Encoding.POLARIZATION)
qutip_bell = converter.to_qutip(pcvl_bell)

# Plot
plot_schmidt(qutip_bell, figsize=(2, 2));

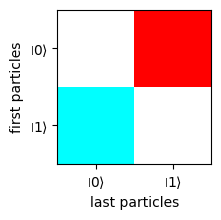
This plot function allows to have a better visualization of entanglement.

Generate a state from a graph

We also developed a tool which takes as input a graph from networkx and provides the associated graph state.

# Create the graph with networkx
G = nx.Graph()
G.add_nodes_from([2,1,0,3])

G.add_edge(0,1)
G.add_edge(1,2)
G.add_edge(2,0)
G.add_edge(2,3)

nx.draw_networkx(G, with_labels=True)

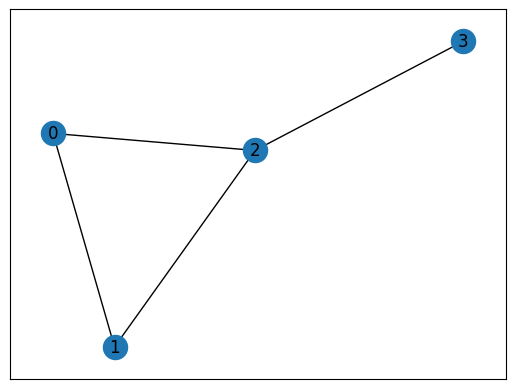
We choose the encoding type we want.

# Set the generator with the dual rail encoding
generator=StateGenerator(Encoding.DUAL_RAIL)

Then we use the generator to create the graph state:

gr_state = generator.graph_state(G)
print(gr_state)

1/4*|0,1,0,1,0,1,0,1>+1/4*|0,1,1,0,1,0,1,0>+1/4*|1,0,0,1,0,1,0,1>-1/4*|0,1,0,1,1,0,0,1>+1/4*|1,0,1,0,1,0,0,1>+1/4*|1,0,0,1,1,0,1,0>+1/4*|1,0,1,0,0,1,1,0>+1/4*|0,1,1,0,1,0,0,1>-1/4*|0,1,1,0,0,1,1,0>-1/4*|1,0,0,1,0,1,1,0>-1/4*|0,1,0,1,0,1,1,0>-1/4*|1,0,1,0,0,1,0,1>+1/4*|1,0,1,0,1,0,1,0>-1/4*|0,1,0,1,1,0,1,0>+1/4*|1,0,0,1,1,0,0,1>+1/4*|0,1,1,0,0,1,0,1>

We can also represent this state with qsphere.

converter = StatevectorConverter(encoding=Encoding.DUAL_RAIL)
qiskit_gr_state = converter.to_qiskit(gr_state)

plot_state_qsphere(qiskit_gr_state)

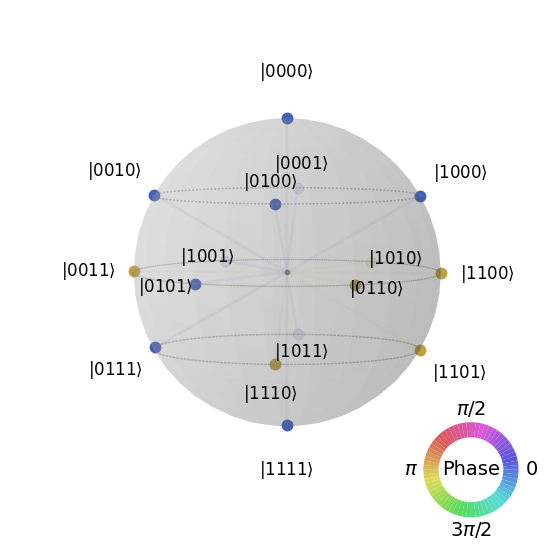
References

[1] Marc Hein et al. “Entanglement in graph states and its applications”. In: arXiv preprint quant-ph/0602096 (2006). https://arxiv.org/abs/quant-ph/0602096

[2] https://qiskit.org/documentation/stubs/qiskit.visualization.plot_state_qsphere.html

[3] https://nbviewer.org/urls/qutip.org/qutip-tutorials/tutorials-v4/visualization/qubism-and-schmidt-plots.ipynb