You're reading the documentation of the v1.0. For the latest released version, please have a look at v1.1.
Processor
Processor is a mean to run a quantum algorithm locally (i.e. on the user’s computer) using a simulation back-end. It contains a linear optics Experiment which can be defined in several ways:
>>> import perceval as pcvl
>>> p = pcvl.Processor("SLOS", 4, name="my proc") # Creates a 4-modes Processor named "my proc" that will be simulated using SLOS
>>> p.m
4
A processor can be created empty with a given number of modes, or using a circuit, or an Experiment.
>>> p = pcvl.Processor("SLOS", pcvl.BS()) # Creates a 2-modes Processor with a single beam splitter as component
Processor composition
Components, circuits and experiments can be added to processors using the add() method
(note however that // doesn’t work for processors).
When another Processor is added, only the enclosed Experiment is copied which means that the
right handside back-end is omitted, and only the one from the left processor is kept.
>>> p.add(0, pcvl.PS(3.14)) # Add a phase shifter on mode 0
However, unlike Circuit, non-linear components can also be added to Processors
>>> p.add(1, pcvl.TD(1)) # Adds a time-delay on mode 1
Secondly, the mode on which a component is added has a few more options than just an integer. One can use a list or a dict of integers to map the output of the current processor to the input of the added component. If the left processor has output ports and the right processor has input ports, it can also be a dict describing the port names.
This adds up a permutation before inserting the new component, and its inverse at the end (so modes don’t move when doing this).
Note however that when adding a processor with asymmetrical heralds (see below),
the inverse permutation is not added since it doesn’t exist, so modes might move (check with a pdisplay).
>>> p.add([1, 0], pcvl.BS(theta=0.7)) # Left mode 1 will connect to right mode 0, and left mode 0 will connect to right mode 1
>>> p.add({1: 0, 0: 1}, pcvl.BS(theta=0.7)) # Same as above
Composition is a powerful tool to achieve complex processors:
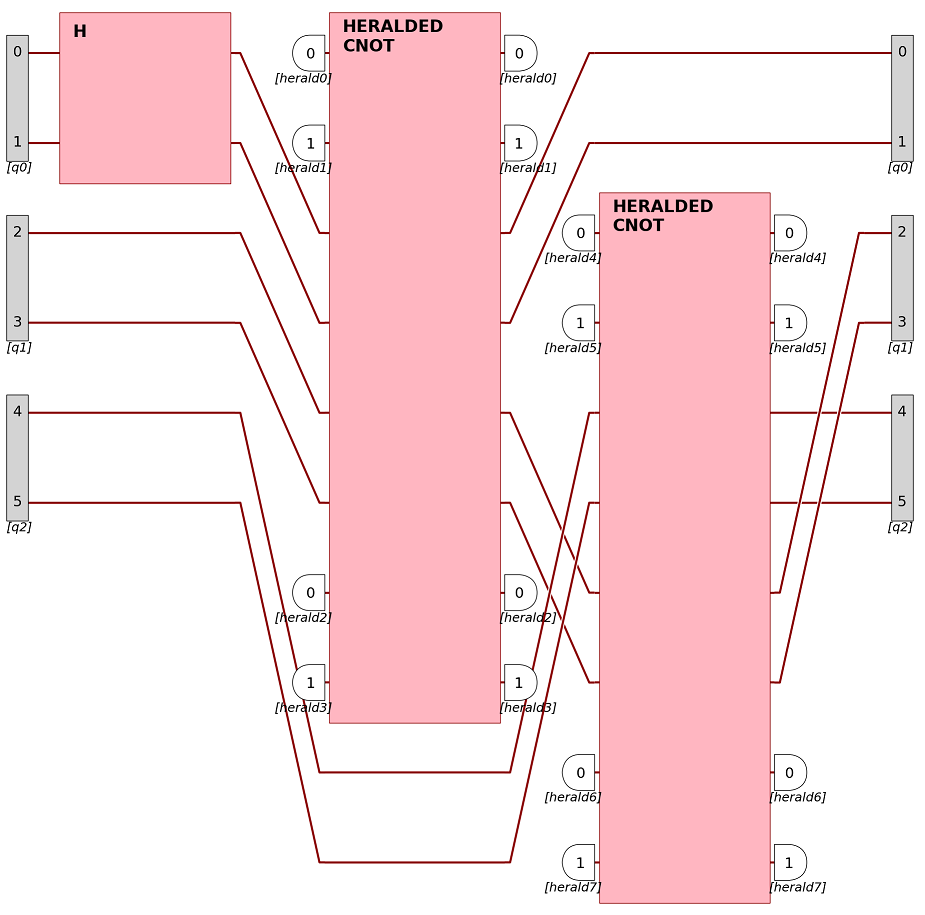
A processor composed of a Hadamard gate and two heralded CNOT gates.
Detectors can also be added to a Processor using the same syntax
>>> p.add(0, pcvl.Detector.threshold())
Once a Detector has been added, no optical component can be added anymore on this mode.
Setting an input state
Before a Processor can be simulated, an input state must be provided.
>>> p.with_input(pcvl.BasicState([1, 0]))
The input state can be:
A
BasicState, in which case the noise from the noise model is computed.A
LogicalStateif ports have been defined, in which case the noise is computed.A
StateVectorA
SVDistribution
If a BasicState has polarization, the method to use is p.with_polarized_input,
and no noise from the source will be applied.
Noise model
Processors can be given noise model to apply noise both on the source and on the components
This noise model can be given at instantiation
>>> p = pcvl.Processor("SLOS", 4, pcvl.NoiseModel(brightness=0.9, phase_error=0.01))
or changed later during the life of a processor
>>> p.noise = pcvl.NoiseModel(brightness=0.8, g2=0.03)
Min photons filter
A threshold on the number of detected photons can be set so outputs having less than this number of photons are filtered out. This has an impact on the perfs of the Processor.
>>> p.min_detected_photons_filter(3) # Outputs will all have at least 3 photons
Ports
Once a Processor has been defined in terms of components, one can add ports and heralds to it. If a port spans over several modes, the specified mode is considered to be the upper one.
>>> p.add_port(0, pcvl.Port(pcvl.Encoding.DUAL_RAIL, "qubit0")) # Adds a dual rail port on modes 0 and 1 on both sides
>>> p.remove_port(0)
>>> p.add_port(0, pcvl.Port(pcvl.Encoding.DUAL_RAIL, "qubit0"), location=pcvl.PortLocation.INPUT) # Add the port on the left of the processor
Ports have three main purposes:
Showing the circuit’s logic in display
Composing processors using ports
Setting an input state
>>> p.with_input(pcvl.LogicalState([0])) # Equivalent to BasicState([1, 0]) for a dual rail. Adapts automatically to the ports
Heralds
Heralds are a special kind of ports that act as modes that the user “doesn’t want to see”.
Note that ports and heralds are mutually exclusive mode-wise.
At the input, they declare a number of photon in a mode that the user won’t have to specify when using with_input.
>>> p = pcvl.Processor("SLOS", pcvl.BS())
>>> p.add_herald(0, 1, location=pcvl.PortLocation.INPUT) # Add an herald of value 1 on input mode 0
>>> p.with_input(pcvl.BasicState([1])) # Only one mode
>>> p.m_in
1
>>> p.heralds_in
{0: 1}
At the output, they will automatically filter states so only states matching the given number of photons will be selected. They also remove these modes from the resulting BasicStates. This filtering has an impact on the perf of the processor.
>>> p = pcvl.Processor("SLOS", pcvl.BS())
>>> p.add_herald(0, 1, location=pcvl.PortLocation.OUTPUT) # Output will have only one mode
>>> p.m
1
>>> p.circuit_size # Real size of the circuit
2
>>> p.heralds
{0: 1}
Heralded output modes can still be seen using p.keep_heralds(True).
In this case, heralded modes can still be removed afterward using state = p.remove_heralded_modes(state)
Heralds at output are independent from the min detected photons filter, as the filter looks only at non-heralded modes.
>>> p.min_detected_photons_filter(2)
>>> p.add_herald(0, 1) # There will actually be at least 3 photons
A Processor that has at least one mode that defines an herald only at input or output is considered asymmetrical.
By default, heralds are added on both sides, so Processors are kept symmetrical.
When composing processors, the processors are considered to have m output modes and m_in input modes.
Heralds are considered to be outside the processors. Thus, they can be moved to new modes to keep a good structure.
Most 2-qubit gates from the catalog are symmetrical processors that use heralds.
When composing with a symmetrical processor, the inverse permutation is added at the right to keep the order of the modes. This is not the case when composing with an asymmetric processor.
>>> from perceval import catalog
>>> p = pcvl.Processor("SLOS", 4)
>>> cnot = catalog["postprocessed cnot"].build_processor()
>>> cnot.m
4
>>> cnot.circuit_size
6
>>> p.add(0, cnot) # Works despite the cnot having 6 modes
>>> p.circuit_size # p is now bigger due to the added heralds from cnot
6
>>> p.heralds
{4: 0, 5: 0}
PostSelect
A post-selection method can be added to a Processor to filter only states matching it.
>>> p.set_postselection(pcvl.PostSelect("[0, 1] == 2"))
>>> p.post_select_fn
[0, 1] == 2
When composing, the modes are swapped to match the new modes of the composition. Also, it is not allowed to add something to an experiment that has a post-selection if the modes overlap one of the nodes of the post-selection (they should be entirely included or disjoint)
If the user knows what they are doing,
they can remove the post-selection using p.clear_postselection() then apply it again.
Note
Processor and RemoteProcessor expose the same behaviour in many ways, and most of the time, when a Processor is needed, it can be replaced with a RemoteProcessor, making the processor to write switch from local to remote computation back and forth as easy as possible.
Computation
Depending on the backend that was specified at the beginning, a Processor can perform probability computation or sampling.
>>> p = pcvl.Processor("SLOS", 4)
>>> p.available_commands
["probs"]
>>> p = pcvl.Processor("CliffordClifford2017", 3)
>>> p.available_commands
["samples"]
Any of the available methods can be used to compute the results for this processor, taking into account the components, the input state, the noise, the heralds, the post-selection…
In any case, the results is a dict containing the results in the field “results” and some performance score corresponding to the probability of getting a selected state.
>>> p = pcvl.Processor("SLOS", pcvl.BS())
>>> p.with_input(pcvl.BasicState([1, 0]))
>>> p.probs()["results"]
BSDistribution(float, {|1,0>: 0.5, |0,1>: 0.5})
- class perceval.components.processor.Processor(backend, m_circuit=None, noise=None, name='Local processor')
Generic definition of processor as an experiment + simulation backend
- Parameters:
backend – Name or instance of a simulation backend
m_circuit (
Union[int,ACircuit,Experiment,None]) –can either be:
- an int: number of modes of interest (MOI). A mode of interest is any non-heralded mode.
>>> p = Processor("SLOS", 5)
- a circuit: the input circuit to start with. Other components can still be added afterwards with add()
>>> p = Processor("SLOS", BS() // PS() // BS())
- an experiment:
>>> p = Processor("SLOS", Experiment(BS(), NoiseModel(0.8)))
noise (
Optional[NoiseModel]) – a NoiseModel containing noise parameters (defaults to no noise)name (
str) – a textual name for the processor (defaults to “Local processor”)
- add(mode_mapping, component, keep_port=True)
Add a component to the processor (unitary or non-unitary).
- Parameters:
mode_mapping –
Describe how the new component is connected to the existing processor. Can be:
an int: composition uses consecutive modes starting from mode_mapping
a list or a dict: describes the full mapping of length the input mode count of component
component –
The component to append to the processor. Can be:
A unitary circuit
A non-unitary component
A processor
A detector
keep_port (
bool) – if True, saves self’s output ports on modes impacted by the new component, otherwise removes them.
- Return type:
AProcessor
Adding a component on non-ordered, non-consecutive modes computes the right permutation (PERM component) which fits into the existing processor and the new component.
Example:
>>> p = Processor("SLOS", 6) >>> p.add(0, BS()) # Modes (0, 1) connected to (0, 1) of the added beam splitter >>> p.add([2,5], BS()) # Modes (2, 5) of the processor's output connected to (0, 1) of the added beam splitter >>> p.add({2:0, 5:1}, BS()) # Same as above
- add_herald(mode, expected, name=None, location=PortLocation.IN_OUT)
Add a heralded mode
- Parameters:
mode (
int) – Mode index of the heraldexpected (
int) – number of expected photon as input and/or output on the given modename (
Optional[str]) – Herald port name. If none is passed, the name is auto-generatedlocation (
PortLocation) – Port location of the herald (input, output or both)
- Return type:
AProcessor
- check_input(input_state)
Check if a Fock state input matches with the current processor configuration
- property circuit_size: int
- Returns:
Total size of the enclosed circuit (i.e. self.m + heralded mode count)
- compute_physical_logical_perf(value)
Tells the simulator to compute or not the physical and logical performances when possible
- Parameters:
value (
bool) – True to compute the physical and logical performances, False otherwise.
- flatten(max_depth=None)
List all the components in the processor where recursive circuits have been flattened.
- Parameters:
max_depth – The maximum depth of recursion. The remaining sub-circuits at this depth are listed as a component.
- Return type:
list[tuple]
- property heralds
- Returns:
A dictionary {mode: expected_count} describing the heralds on the output
- property in_heralds
- Returns:
A dictionary {mode: expected_count} describing the heralds on the input
- property in_port_names
- Returns:
A list of the input port names. Names are repeated for ports connected to more than one mode
- linear_circuit(flatten=False)
Creates a linear circuit from internal components, if all internal components are unitary. Takes phase imprecision noise into account.
- Parameters:
flatten (
bool) – if True, the component recursive hierarchy is discarded, making the output circuit “flat”.- Raises:
RuntimeError – If any component is non-unitary
- Return type:
- Returns:
The resulting Circuit object
- log_resources(method, extra_parameters)
Log resources of the processor
- Parameters:
method (
str) – name of the method usedextra_parameters (
dict) –extra parameters to log.
Extra parameter can be:
max_samples
max_shots
precision
- property m: int
- Returns:
The number of modes that are free (non-heralded) on the output
- property m_in: int
- Returns:
The number of modes that are free (non-heralded) on the input, that must be specified when using self.with_input()
- min_detected_photons_filter(n)
Sets-up a state post-selection on the number of detected photons. With threshold detectors, this will actually filter on “click” count.
- Parameters:
n (
int) – Minimum expected photons. Does not take heralded modes into account.
This post-selection has an impact on the output physical performance
- property out_port_names
- Returns:
A list of the output port names. Names are repeated for ports connected to more than one mode
- set_circuit(circuit)
Removes all components and replace them by the given circuit.
- Parameters:
circuit (
ACircuit) – The circuit to start the processor with- Return type:
AProcessor- Returns:
Self to allow direct chain this with .add()
- set_postselection(postselect)
Set a logical post-selection function. Along with the heralded modes, this function has an impact on the logical performance of the processor
- Parameters:
postselect (
PostSelect) – Sets a post-selection function. Its signature must be func(s: BasicState) -> bool. If None is passed as parameter, removes the previously defined post-selection function.
- property source
- Returns:
The photonic source
- property source_distribution: SVDistribution | None
Retrieve the computed input distribution. Compute it if it is not cached and an input state has been provided. :return: the input SVDistribution if with_input was called previously, otherwise None.
- with_input(input_state)
Simulates plugging the photonic source on certain modes and turning it on. Computes the input probability distribution
- Parameters:
input_state (
BasicState|LogicalState|StateVector|SVDistribution) – Expected input BasicState, StateVector or SVDistribution of length self.m (heralded modes are managed automatically), or a LogicalState with length ‘number of non-herald ports or port-free modes’.
The properties of the source will alter the input state for BasicState and LogicalState inputs. A perfect source always delivers the expected state as an input. Imperfect ones won’t.