Unitary Components

Overview

Name	Class Name	Unitary Matrix
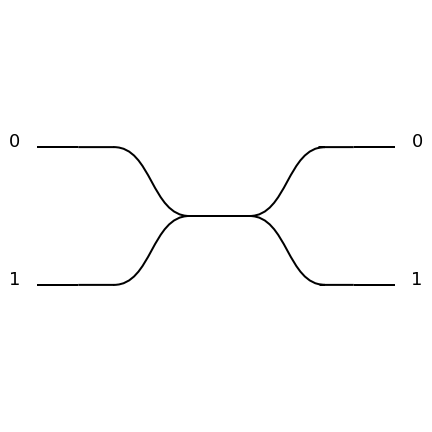
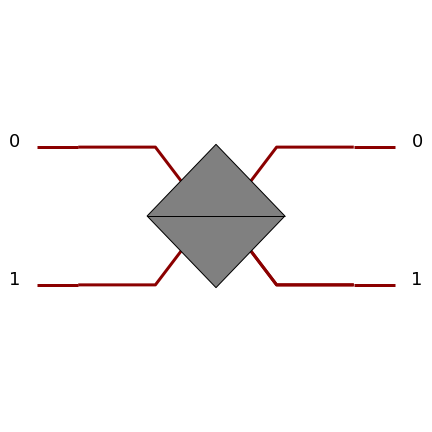
Beam Splitter	`BS`	Depends on the convention, see Beam Splitter
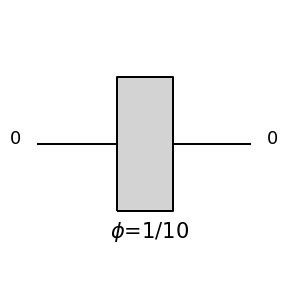
Phase Shifter	`PS`	\(\left[\begin{matrix}e^{i \phi}\end{matrix}\right]\)
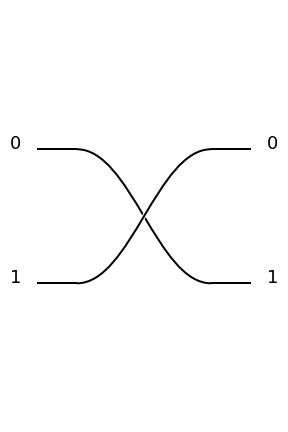
Permutation	`PERM`	Example of a two mode permutation: \(\left[\begin{matrix}0 & 1\\1 & 0\end{matrix}\right]\)
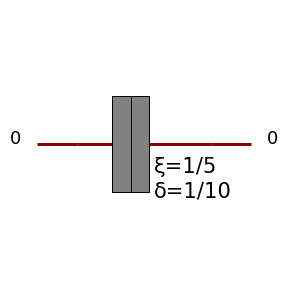
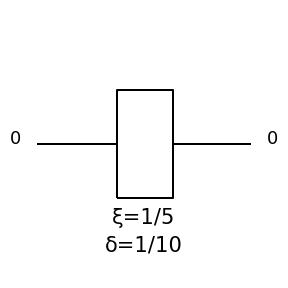
Wave Plate	`WP`	\(\left[\begin{matrix}i \sin{\left(\delta \right)} \cos{\left(2 \xi \right)} + \cos{\left(\delta \right)} & i \sin{\left(\delta \right)} \sin{\left(2 \xi \right)}\\i \sin{\left(\delta \right)} \sin{\left(2 \xi \right)} & - i \sin{\left(\delta \right)} \cos{\left(2 \xi \right)} + \cos{\left(\delta \right)}\end{matrix}\right]\)
Polarising Beam Splitter	`PBS`	\(\left[\begin{matrix}0 & 0 & 1 & 0\\0 & 1 & 0 & 0\\1 & 0 & 0 & 0\\0 & 0 & 0 & 1\end{matrix}\right]\)
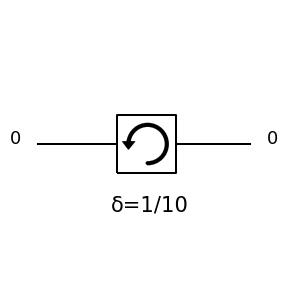
Polarisation Rotator	`PR`	\(\left[\begin{matrix}\cos{\left(\delta \right)} & \sin{\left(\delta \right)}\\- \sin{\left(\delta \right)} & \cos{\left(\delta \right)}\end{matrix}\right]\)

Beam Splitter

Beam Splitter conventions

enum perceval.components.unitary_components.BSConvention(value)

Beam splitter conventions

Member Type:: int

Valid values are as follows:

Rx = <BSConvention.Rx: 0>

Ry = <BSConvention.Ry: 1>

H = <BSConvention.H: 2>

Three specialised conventions are defined, with a single \(\theta\) parameter, as follow:

Convention	Unitary matrix	Default value (\(\theta=\pi/2\))	Comment
`Rx`	\(\left[\begin{matrix}\cos{(\theta/2)} & i \sin{(\theta/2)}\\i \sin{(\theta/2)} & \cos{(\theta/2)}\end{matrix}\right]\)	\(\left[\begin{matrix}1 & i\\i & 1\end{matrix}\right]\)	Symmetrical, default convention
`Ry`	\(\left[\begin{matrix}\cos{(\theta/2)} & -\sin{(\theta/2)}\\ \sin{(\theta/2)} & \cos{(\theta/2)}\end{matrix}\right]\)	\(\left[\begin{matrix}1 & -1\\1 & 1\end{matrix}\right]\)	Real, non symmetrical
`H`	\(\left[\begin{matrix}\cos{(\theta/2)} & \sin{(\theta/2)}\\ \sin{(\theta/2)} & -\cos{(\theta/2)}\end{matrix}\right]\)	\(\left[\begin{matrix}1 & 1\\1 & -1\end{matrix}\right]\)	Hadamard gate, `HH=I`, non symmetrical

Each convention also accepts up to four additional phases, mimicking a phase shifter on each mode connected to the beam splitter. For instance, with the Rx convention, the unitary matrix is defined by:

\(\left[\begin{matrix}e^{i(\phi_{tl}+\phi_{tr})} \cos{\left(\theta/2 \right)} & i e^{i (\phi_{tr}+\phi_{bl})} \sin{\left(\theta/2 \right)}\\i e^{i \left(\phi_{tl} + \phi_{br}\right)} \sin{\left(\theta/2 \right)} & e^{i (\phi_{br}+\phi_{bl})} \cos{\left(\theta/2 \right)}\end{matrix}\right]\)

It is thus parametrized by \(\theta\), \(\phi_{tl}\), \(\phi_{bl}\), \(\phi_{tr}\) and \(\phi_{br}\) angles, making this beam splitter equivalent to:

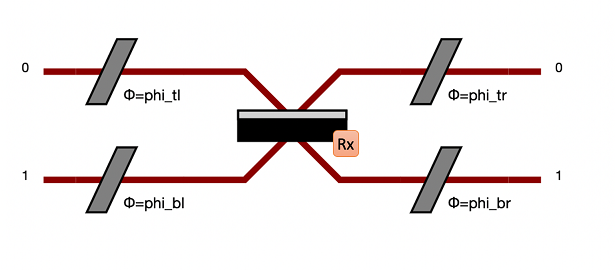
Beam Splitter reflectivity

\(\theta\) relates to the reflectivity and \(\phi\) angles correspond to relative phases between modes. Beam splitters exist as bulk, fibered and on-chip components.

The relationship between the reflectivity \(R\) and \(\theta\) is: \(cos {\left( \theta/2 \right)} = \sqrt{R}\).

To create a beam splitter object with a given reflectivity value:

>>> from perceval.components import BS
>>> R = 0.45
>>> beam_splitter = BS(BS.r_to_theta(R))

Beam Splitter code reference

class perceval.components.unitary_components.BS(theta=pi / 2, phi_tl=0, phi_bl=0, phi_tr=0, phi_br=0, convention=BSConvention.Rx)

Beam Splitter

Beam splitters couple two spatial modes together, acting on \(\ket{1,0}\) and \(\ket{0,1}\).

Parameters:

theta (Parameter | float) – theta parameter
phi_tl (Parameter | float) – top-left phase parameter
phi_bl (Parameter | float) – bottom-left phase parameter
phi_tr (Parameter | float) – top-right phase parameter
phi_br (Parameter | float) – bottom-right phase parameter

static H(theta=pi / 2, phi_tl=0, phi_bl=0, phi_tr=0, phi_br=0): Convenient named constructor for a Beam Splitter following Hadamard convention. Its parameters are the same as the main constructor.

static Rx(theta=pi / 2, phi_tl=0, phi_bl=0, phi_tr=0, phi_br=0): Convenient named constructor for a Beam Splitter following Rotation X convention. Its parameters are the same as the main constructor.

static Ry(theta=pi / 2, phi_tl=0, phi_bl=0, phi_tr=0, phi_br=0): Convenient named constructor for a Beam Splitter following Rotation Y convention. Its parameters are the same as the main constructor.

property U: get the symbolic unitary matrix

assign(assign=None)

Assign values to parameters referenced in assign

Parameters:: assign (dict[str, float | int]) – A dictionary mapping parameter_name -> value. Set the value to the parameter whose name is parameter_name for each key of the dictionary.
Raises:: KeyError – If parameter_name is not an existing variable parameter name of the circuit.

compute_unitary(assign=None, use_symbolic=False, use_polarization=None)

Compute the unitary matrix corresponding to the current circuit

Parameters:

use_polarization (bool | None) – ask for polarized circuit to double size unitary matrix
assign (dict) – optional mapping between parameter names and their corresponding values
use_symbolic (bool) – if the matrix should use symbolic calculation

Return type:

Matrix

Returns:

the unitary matrix, will be a MatrixS if symbolic, or a ~`MatrixN` if not.

property convention: Beam splitter convention

property defined: bool: check if all parameters of the circuit are fully defined

definition()

Gives mathematical definition of the circuit

Only defined for elementary circuits

depths()

Returns:: the depth of the circuit for each mode

describe()

Describe the component as the Python code that generates it.

Return type:: str
Returns:: code generating the component

get_parameters(all_params=False, expressions=False)

Return the parameters of the component

Parameters:

all_params (bool) – if False, only returns the variable parameters
expressions – if True, returns Expressions and parameters embedded in circuit components. If False, returns the raw parameters that make up the expressions only. Default False.

Return type:

list[Parameter]

Returns:

the list of parameters

property name: Returns component name

ncomponents()

Returns:: number of actual components in the circuit

param(param_name): Extract a Parameter object from its name :type param_name: str :param param_name: The name of the parameter :rtype: Parameter :return: A Parameter object

property params: Iterable[str]

Returns:: a list of all variable parameter names in the component

static r_to_theta(r)

Compute theta given a reflectivity value. Supports symbolic computing.

Parameters:: r (float | Parameter) – reflectivity value (can be variable)
Return type:: float | Expression
Returns:: theta value or symbolic expression

property reflectivity

Beam Splitter reflectivity

Returns:: reflectivity of the current Beam Splitter

property requires_polarization

Does the circuit require polarization?

Returns:: is True if the circuit has a polarization component

static theta_to_r(theta)

Compute reflectivity given a theta value. Supports symbolic computing.

Parameters:: theta (float | Parameter) – theta angle (can be variable)
Return type:: float | Expression
Returns:: reflectivity value or symbolic expression

property vars: dict[str, perceval.utils.parameter.Parameter]

Returns:: A dictionary mapping parameter names to parameters for all variable parameters of the circuit

Phase Shifter

class perceval.components.unitary_components.PS(phi, max_error=0)

Phase shifter

A phase shifter adds a phase \(\phi\) on a spatial mode, which corresponds to a Z rotation in the Bloch sphere.

Parameters:

phi (Parameter | float) – Phase angle
max_error (Parameter | float) – Maximum random error to apply. The error is uniformly drawn in \([\phi - max_{error}, \phi + max_{error}]\). A global phase error noise parameter can also be set in the NoiseModel for all the phase shifters of a given Experiment.

definition()

Gives mathematical definition of the circuit

Only defined for elementary circuits

Return type:: Matrix

describe()

Describe the component as the Python code that generates it.

Returns:: code generating the component

Permutation

A permutation swaps multiple consecutive spatial modes.

To create a permutation PERM sending \(\ket{0,1}\) to \(\ket{1,0}\) and vice-versa:

>>> from perceval.components import PERM
>>> permutation = PERM([1, 0])

More generally, one can define a permutation on an arbitrary number of modes. The permutation is described by a list of integers from 0 to \(l-1\), where \(l\) is the length of the list. The \(k^{th}\) spatial input mode is sent to the spatial output mode corresponding to the \(k\) th value in the list.

For instance the following defines a 4-mode permutation. It matches the first input path (index 0) with the third output path (value 2), the second input path with the fourth output path, the third input path, with the first output path, and the fourth input path with the second output path.

>>> import perceval as pcvl
>>> import perceval.components.unitary_components as comp
>>> c = comp.PERM([2, 3, 1, 0])
>>> pcvl.pdisplay(c)
>>> pcvl.pdisplay(c.compute_unitary(), output_format=pcvl.Format.LATEX)

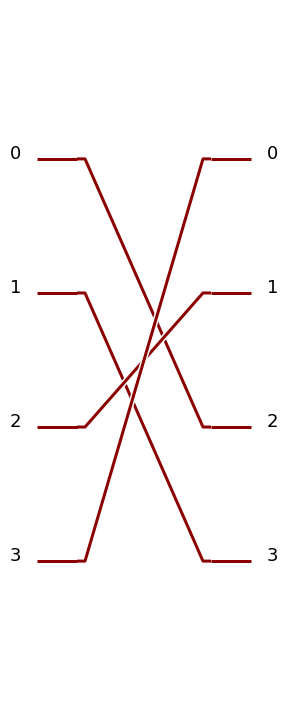
\[\begin{split}\left[\begin{matrix}0 & 0 & 0 & 1\\0 & 0 & 1 & 0\\1 & 0 & 0 & 0\\0 & 1 & 0 & 0\end{matrix}\right]\end{split}\]

class perceval.components.unitary_components.PERM(perm)

Permutation

A swap between any number of consecutive spatial modes.

Parameters:: perm (list[int]) – Vector of mode index defining the permutation.

>>> permutation = PERM([2, 3, 1, 0])  # respectively swaps mode 0 to 2, 1 to 3, 2 to 1 and 3 to 0.

apply(r, sv)

Apply the permutation to a state

Parameters:: r (tuple[int, ...]) – Range of consecutive modes where the permutation occurs
Sv:: State on which the permutation is applied

break_in_2_mode_perms()

Breaks any n-mode permutation into an equivalent circuit made of only 2-mode permutations.

Returns:: An equivalent Circuit made of only 2-mode permutations

definition()

Gives mathematical definition of the circuit

Only defined for elementary circuits

describe()

Describe the component as the Python code that generates it.

Returns:: code generating the component

property perm_vector: Return the permutation vector

Unitary

class perceval.components.unitary_components.Unitary(U, name=None, use_polarization=False)

Generic component defined by a unitary matrix

Parameters:

U (Matrix) – numeric matrix. Does not support symbolic computation.
name (Optional[str]) – Custom name for the component it represents (default is “Unitary”).
use_polarization (bool) – True if the unitary represents a polarized component.

describe()

Describe the component as the Python code that generates it.

Returns:: code generating the component

Wave Plate

class perceval.components.unitary_components.WP(delta, xsi)

A wave plate acts on the polarisation modes of a single spatial mode. This component acts on polarised photons. See also: Polarisation

Parameters:

delta (float | Parameter) – parameter proportional to the thickness of the waveplate
xsi (float | Parameter) – angle of the waveplate’s optical axis in the \(\left\{\ket{H}, \ket{V}\right\}\) plane. Especially important is the case that \(\delta=\pi/2\), known as a half-wave plate, which rotates linear polarisations in the \(\left\{\ket{H}, \ket{V}\right\}\) plane.

describe()

Describe the component as the Python code that generates it.

Returns:: code generating the component

class perceval.components.unitary_components.HWP(xsi)

Half wave plate

This component acts on polarized photons. See also: Polarization

definition()

Gives mathematical definition of the circuit

Only defined for elementary circuits

class perceval.components.unitary_components.QWP(xsi)

Quarter wave plate

This component acts on polarized photons. See also: Polarization

definition()

Gives mathematical definition of the circuit

Only defined for elementary circuits

Polarisation Rotator

class perceval.components.unitary_components.PR(delta)

A polarisation rotator is an optical device that rotates the polarization axis of a linearly polarized light beam by an angle of choice. Such devices can be based on the Faraday effect, on bi-refringence, or on total internal reflection. Rotators of linearly polarized light have found widespread applications in modern optics since laser beams tend to be linearly polarized. It is often necessary to rotate the original polarization to its orthogonal alternative. This component acts on polarized photons. See also: Polarization

See https://en.wikipedia.org/wiki/Polarization_rotator for more details.

Parameters:: delta (float | Parameter) – Rotation angle

describe()

Describe the component as the Python code that generates it.

Returns:: code generating the component

Polarising Beam Splitter

class perceval.components.unitary_components.PBS

A polarising beam splitter converts a superposition of polarisation modes in a single spatial mode to the corresponding equal-polarisation superposition of two spatial modes, and vice versa, and so in this sense allows us to translate between polarisation and spatial modes. The unitary matrix associated to a polarising beam splitter acting on the tensor product of the spatial mode and the polarisation mode is:

\(\left[\begin{matrix}0 & 0 & 1 & 0\\0 & 1 & 0 & 0\\1 & 0 & 0 & 0\\0 & 0 & 0 & 1\end{matrix}\right]\)

This component acts on polarized photons. See also: Polarization

describe()

Describe the component as the Python code that generates it.

Returns:: code generating the component

Barrier

class perceval.components.unitary_components.Barrier(m, visible=True)

A barrier is a visual component which has no effect on photons (it behaves as an identity unitary). It may be used to separate or align multiple components in a given Circuit.

Parameters:

m (int) – Number of consecutive modes it covers
visible (bool) – The barrier is rendered if True, and is invisible otherwise

definition()

Gives mathematical definition of the circuit

Only defined for elementary circuits

describe()

Describe the component as the Python code that generates it.

Returns:: code generating the component