You're reading the documentation of the v0.10. For the latest released version, please have a look at v0.11.

Tools

Parameters

Parameters are to way to parameterize circuits - See Parameter for the full class documentation.

Defining Parameters and reading/writing their values

To define a parameter - just do:

>>> alpha = perceval.P("alpha")

When defining the parameter, you can also set its value, and max/min values and periodicity:

>>> alpha = perceval.P("phi", min_v=0, max_v=2*math.pi, periodic=True)

defining boundaries and periodicity is used in particular when optimizing a parameterized circuit.

Using parameters in a circuit

When a parameter is defined, you can use it within a circuit:

>>> c = BS(theta=alpha)

You can use it several times and define other parameters dynamically:

>>> c = BS(theta=alpha) // PS(pcvl.P("phi")) // BS(theta=alpha)

Note

If you declare two parameters with the same name, they are not referring to the same variable, and to avoid confusion you can not use them simultaneously in a same circuit - the following is incorrect:

>>> c = BS(theta=pcvl.P("alpha")) // PS(pcvl.P("phi")) // BS(theta=pcvl.P("alpha"))

You can retrieve the parameters used in a circuit as following:

>>> params = c.get_parameters()
[Parameter(name='alpha_1', value=None, min=0.0, max=6.283185307179586),
 Parameter(name='phi', value=None, min=0.0, max=6.283185307179586),
 Parameter(name='alpha2', value=None, min=0.0, max=6.283185307179586)]

Setting Values

To give a value to a parameter, use set_value:

>>> alpha.set_value(math.pi/4)

The parameter is then defined and its value will be used when calculating circuit unitary:

>>> alpha.defined
True
>>> pcvl.pdisplay(c.compute_unitary(use_symbolic=False))
⎡sqrt(2)/2  sqrt(2)/2 ⎤
⎣sqrt(2)/2  -sqrt(2)/2⎦

To “forget” the value and turn back the parameter into a variable, use `reset - or reset_parameters for a circuit

>>> c.reset_parameters()

Visualization

In Perceval, to display anything, we use pcvl.pdisplay().

Display a circuit

Any circuit coded in perceval can be displayed. You just need to make the code associated with the desired circuit, let’s call it circ, and add pcvl.pdisplay(circ) afterwards in the python cell.

Let’s do an example to understand : you want to display the Mach-Zendher Interferometer.

Start by doing the code associated to the circuit.

>>> import perceval.components.unitary_components as comp
>>> mzi = (pcvl.Circuit(m=2, name="mzi")
...        .add((0, 1), comp.BS())
...        .add(0, comp.PS(pcvl.Parameter("phi1")))
...        .add((0, 1), comp.BS())
...        .add(0, comp.PS(pcvl.Parameter("phi2"))))

Then, add pcvl.pdisplay() of your circuit.

>>> pcvl.pdisplay(mzi)

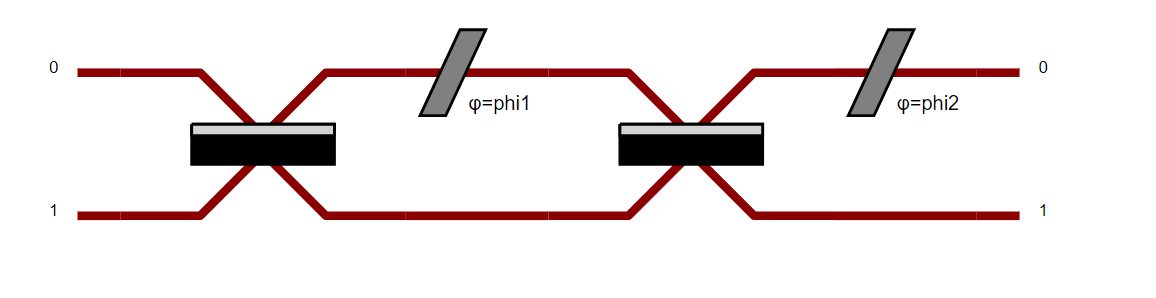
Tip

The outcome of this last command will depend on your environment.

Text Console	Jupyter Notebook	IDE (Pycharm, Spyder, etc)

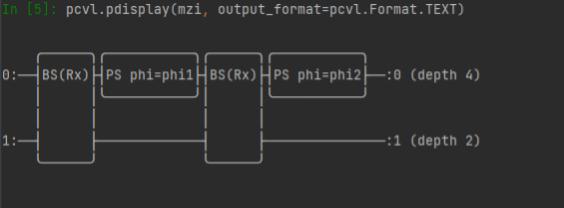
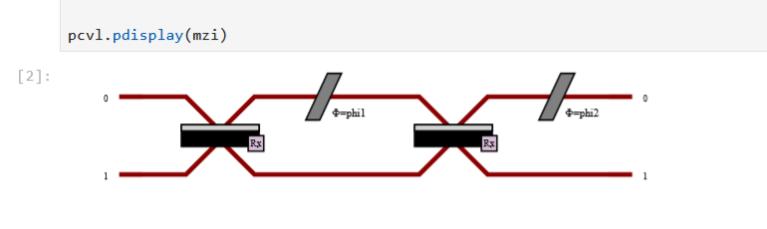
Also, you can change the display of the circuit using a different skin which can itself be configured. Indeed, a boolean can be set to obtain a more compact display (if the circuit is too wide for example).

>>> import perceval as pcvl
>>> import perceval.components.unitary_components as comp
>>> from perceval.rendering.circuit import SymbSkin
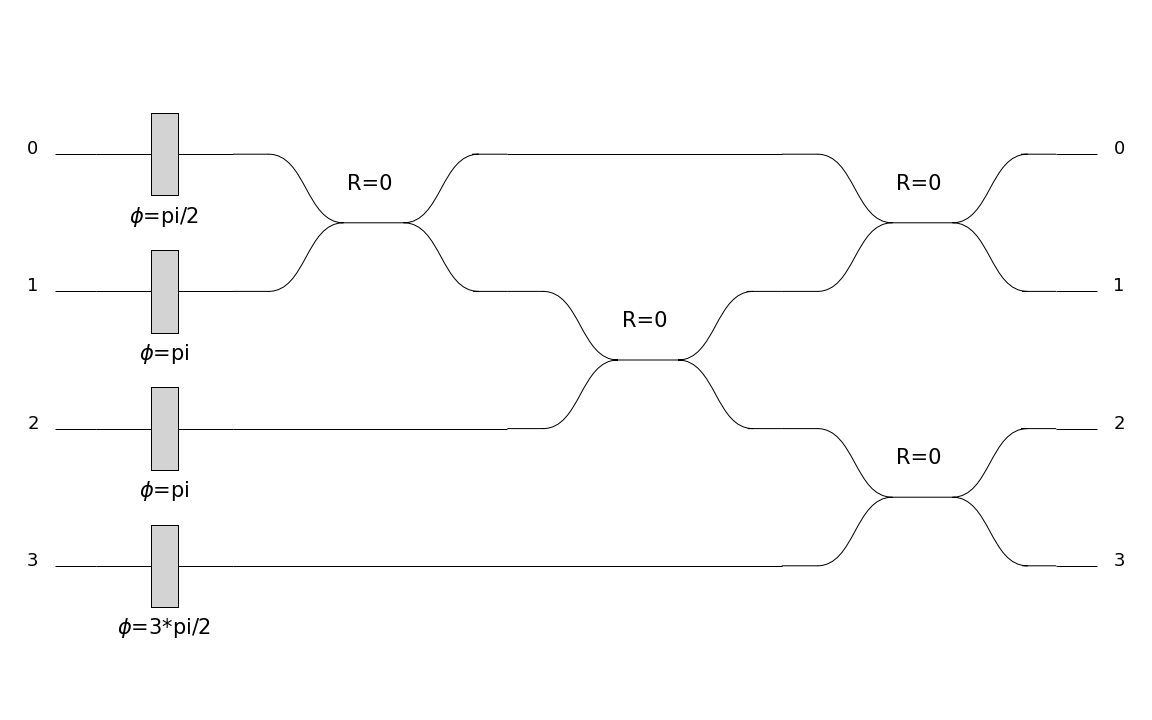
>>> C = pcvl.Circuit.decomposition(pcvl.Matrix(comp.PERM([3, 1, 0, 2]).U),
>>> comp.BS(R=pcvl.P("R")), phase_shifter_fn=comp.PS)
>>> symbolic_skin = SymbSkin(compact_display=True)
>>> pcvl.pdisplay(C, skin=symbolic_skin)

>>> symbolic_skin = SymbSkin(compact_display=False)
>>> pcvl.pdisplay(C, skin=symbolic_skin)

_images/decomposition_symb_compact_false.png

Matrices

With Perceval, you can also display the matrix associated to your circuit.

>>> pcvl.pdisplay(mzi.U)

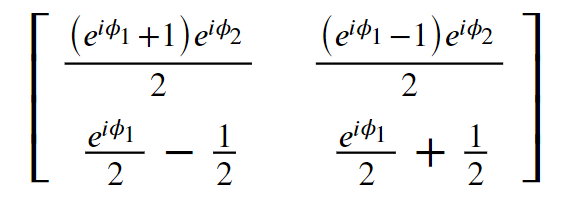
Analyzer algorithm

With Perceval, we can use Analyzer to analyse the circuit and compute the associated output probabilities.

For example, we call the Naive backend that we store in simulator_backend:

>>> simulator_backend = pcvl.BackendFactory().get_backend('Naive')

We can create an input state that will enter our optical scheme later on. We store it in input_state and use BasicState from the Perceval library.

>>> input_state = pcvl.BasicState("|1,1>")

let’s simulate the distribution obtained when we input two photons in a beam-splitter. We will use the Naive backend already stored in simulator_backend.

We will simulate the behavior of the circuit using the Circuit Analyzer which has three arguments:

The first one is an instance of a processor containing the circuit to analyse.
The second one is the input state (we will use input_state).
The third one is the desired output states. To compute all possible output states, one just input “*”.

>>> p = Processor("SLOS", comp.BS())        # create a processor running on SLOS backend
>>> ca = pcvl.algorithm.Analyzer(p,
...                              [input_state],
...                              "*")

Then, we display the result of Circuit Analyzer via pdisplay.

>>> pcvl.pdisplay(ca)

Random numbers

To achieve a reproducible result, for example in notebook execution, the pcvl.random_seed() function can be used at the beginning of the program. This function ensures that any random numbers in the optimisation or random parameter generation functions will be reproducible from run to run.

Let’s do a small example to understand:

>>> pcvl.random_seed(2)
>>> print(random.random())
0.9478274870593494
>>> print(random.random())
0.9560342718892494

>>> pcvl.random_seed(2)
>>> print(random.random())
0.9478274870593494
>>> print(random.random())
0.9560342718892494

Since the seeds of the 2 cells are identical, the randomly generated numbers are also equal. It works the same way with notebook results.

Converters

The perceval.converters package contains useful tools to convert to and from Perceval objects. They act as bridges to other libraries.

Qiskit converter

Serialization

Perceval provides generic functions to serialize / deserialize data. A lot of Perceval data classes come with their optimized serializer (matrixes, circuits, basic states, state vectors and some other specific containers).

>>> import perceval as pcvl
>>> from perceval.serialization import serialize, deserialize
>>> c = pcvl.Circuit(4, "My circuit") // pcvl.Unitary(pcvl.Matrix.random_unitary(4))
...     // PS(phi=pcvl.P("phi_0")) // pcvl.Unitary(pcvl.Matrix.random_unitary(4))
>>> text_repr = serialize(c)
>>> c2 = deserialize(text_repr)  # c and c2 are two instances of the same circuit