First of all I would like to thank you for the development of Perceval and its distribution. It is a very promising tool looking at the different applications you have yielded ! Speaking of which, I would have some question regarding the application on solving differential equation.
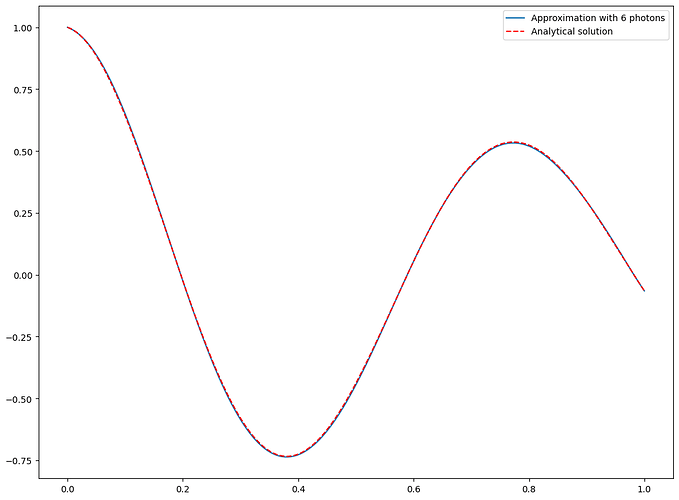
In the reference article you used [2] it is mentioned as you say that increasing the number of photons allows to increase the frequency spectrum and therefore the expressivity of the Fourier series described by the circuit. This leads as you show to an improvement of the approximation of the DE solution.
It is also mentioned in the same article in appendix A but also in [1] that the frequency range can also be increased by changing the spectrum of the operator associated to the encoding layer, or by repeating the same sandwiching L times. In your example you only have one phase shift exp(ix) in the first mode, but one can also try to add 4 additional phase shifts exp(i(k+1)x) in the mode k, k being from 1 to (m-2). Here is a notebook (I cannot share the file so here is the result)
adding this, which also shows a much better agreement with same number of modes and photons. I guess the goal of the notebook was to show the evolution with the number of photons, which might be more visible with only one phase shift. Nevertheless the articles in reference are very (very) rich and a note in the notebook could provide even better prospects for the scalability on multidimensional Fourier series from your notebooks.
In addition I also wanted to understand some points that I missed in the implementation. [2] mentions the importance to add a regularization term in the cost function in case of noise for hardware evaluation. This brings me to my question regarding the intriguing definitions of the parameters « lambda_random » and « a » defined at the top of the notebook. I guess « a » is a simple scaling factor necessary for the Fourier coefficients scaling possibilities, do you have more explanations on those two parameters ? Also you mention that the parameters lambda are tunable but may I ask what for ? Also since they do not enter the minimisation procedure here, how these not-trained parameters are involved in regularization mentioned in formula 11 of [2] ?
The last points are still fuzzy for me so excuse me if I totally missed the point here ![]()
Thanks a lot for your explanations. Also I am currently working on the implementation of a basic classification algorithm based on the very same scheme and golden articles on the moon and circle datasets, that I would be glad to discuss for improvements and share.
Cheers,
Brian Ventura
[1] Schuld, M., Sweke, R., & Meyer, J. J. (2021). The effect of data encoding on the expressive power of variational quantum machine learning models.
[2] Yee Gan, B., Leykam, D., & Angelakis, D. G. (n.d.). Fock State-enhanced Expressivity of Quantum Machine Learning Models.