{
"cells": [
{
"cell_type": "markdown",
"id": "29990c15",
"metadata": {},
"source": [
"# CHSH experiment"
]
},
{
"cell_type": "markdown",
"id": "c1e5e2ac",
"metadata": {},
"source": [
"In this notebook, we aim to reproduce the $\\mathsf{CNOT}$ Gate to \n",
"evaluate its performance while demonstrating key features of Perceval. We use as basis the implementation from [[1]](#Reference)."
]
},
{
"cell_type": "code",
"execution_count": 1,
"id": "bb751c13",
"metadata": {},
"outputs": [],
"source": [
"import math\n",
"\n",
"import perceval as pcvl"
]
},
{
"cell_type": "markdown",
"id": "cb91de5c",
"metadata": {},
"source": [
"### Ralph CNOT Gate"
]
},
{
"cell_type": "markdown",
"id": "d1d6cd32",
"metadata": {},
"source": [
"We start by building the circuit as defined by the paper above - it is a circuit on six modes (labelled from 0 to 5 from top to bottom) consisting of five beam splitters. Modes 0 and 1 contain the control system while modes 2 and 3 encode the target system. Modes 4 and 5 are unoccupied ancillary modes (they are not displayed, but they are required)."
]
},
{
"cell_type": "code",
"execution_count": 2,
"id": "edafa605",
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"\n",
""
],
"text/plain": [
""
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = pcvl.catalog['postprocessed cnot'].build_processor()\n",
"\n",
"pcvl.pdisplay(p, recursive=True)"
]
},
{
"cell_type": "markdown",
"id": "0290b85a",
"metadata": {
"collapsed": false
},
"source": [
"Simulations will run on this circuit, using four different input states corresponding to the two-qubit computational basis states. The `Analyzer` is used to compute the gate performance."
]
},
{
"cell_type": "code",
"execution_count": 3,
"id": "87a00b53",
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
00
01
10
11
\n",
"\n",
"\n",
"
00
1
0
0
0
\n",
"
01
0
1
0
0
\n",
"
10
0
0
0
1
\n",
"
11
0
0
1
0
\n",
"\n",
"
"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"performance = 1/9, fidelity = 100.0%\n"
]
}
],
"source": [
"states = {\n",
" pcvl.BasicState([1, 0, 1, 0]): \"00\",\n",
" pcvl.BasicState([1, 0, 0, 1]): \"01\",\n",
" pcvl.BasicState([0, 1, 1, 0]): \"10\",\n",
" pcvl.BasicState([0, 1, 0, 1]): \"11\"\n",
"}\n",
"\n",
"ca = pcvl.algorithm.Analyzer(p, states)\n",
"ca.compute(expected={\"00\": \"00\", \"01\": \"01\", \"10\": \"11\", \"11\": \"10\"})\n",
"pcvl.pdisplay(ca)\n",
"print(f\"performance = {pcvl.simple_float(ca.performance)[1]}, fidelity = {ca.fidelity*100}%\")"
]
},
{
"cell_type": "markdown",
"id": "0cd5fcf4",
"metadata": {},
"source": [
"Beyond the actual logic function, what is interesting with this gate us that it produces entangled states that we will be trying to check with CHSH experiment when the source is not perfect."
]
},
{
"cell_type": "markdown",
"id": "c0fb4c12",
"metadata": {},
"source": [
"### Checking for entanglement with CHSH experiment\n",
"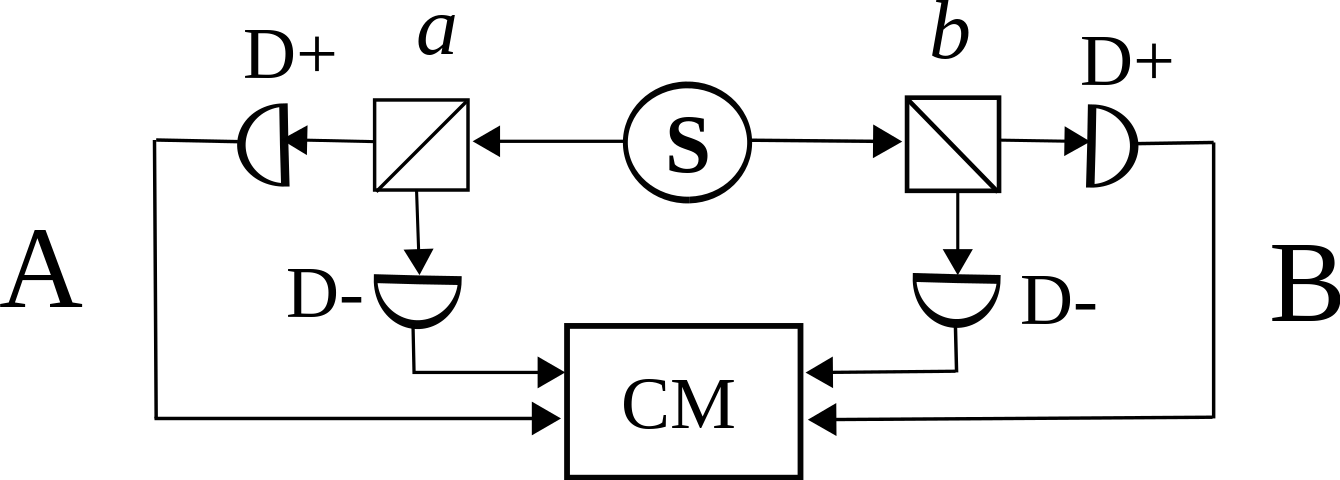\n",
"*https://en.wikipedia.org/wiki/File:Two_channel_bell_test.svg*"
]
},
{
"cell_type": "markdown",
"id": "4e523cfc",
"metadata": {},
"source": [
"To reproduce this Bell test protocol, we define a new circuit which uses the $\\mathsf{CNOT}$ gate implemented above as a sub-circuit. The parameters $a$ and $b$ describe the measurement bases used by players $A$ and $B$ in the runs of the Bell-test. We define a noise model that represent a photon source with a brightness of 40% and a purity of 99% that will be used by the `Processor`."
]
},
{
"cell_type": "code",
"execution_count": 4,
"id": "6b889867",
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"\n",
""
],
"text/plain": [
""
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"noise = pcvl.NoiseModel(brightness=0.4, g2=0.01)\n",
"\n",
"QPU = pcvl.Processor(\"SLOS\", 4, noise=noise)\n",
"QPU.add(0, pcvl.BS.H())\n",
"QPU.add(0, p)\n",
"\n",
"a = pcvl.Parameter(\"a\")\n",
"b = pcvl.Parameter(\"b\")\n",
"\n",
"QPU.add(0, pcvl.BS.H(theta=a))\n",
"QPU.add(2, pcvl.BS.H(theta=b))\n",
"\n",
"pcvl.pdisplay(QPU, recursive=True)"
]
},
{
"cell_type": "markdown",
"id": "1c96eaec",
"metadata": {},
"source": [
"We start by setting the values of the two parameters to 0, meaning that the beam splitters after the $\\mathsf{CNOT}$ effectively act as the identity. "
]
},
{
"cell_type": "code",
"execution_count": 5,
"id": "1e935739",
"metadata": {},
"outputs": [],
"source": [
"a.set_value(0)\n",
"b.set_value(0)"
]
},
{
"cell_type": "markdown",
"id": "3451e7d1",
"metadata": {},
"source": [
"We now state that our photons will be inputted on ports 0 and 2 (using the 0-index convention, and not counting heralded modes)."
]
},
{
"cell_type": "code",
"execution_count": 6,
"id": "1b626655",
"metadata": {},
"outputs": [],
"source": [
"QPU.min_detected_photons_filter(2)\n",
"QPU.with_input(pcvl.BasicState([1, 0, 1, 0]))"
]
},
{
"cell_type": "markdown",
"id": "fcdef3f6",
"metadata": {},
"source": [
"We now detail the different state vectors that are the probabilistic inputs to the circuit. The most frequent input is the empty state, followed by two states with only a single photon on either of the input ports, then by the expected nominal input $|1,0,1,0,0,0\\rangle$. Here, the heralded modes are shown because if there were a photon on them, they would also have the imperfect source. They are represented at the end of the state (the two last modes) as they have been added after the declaration of the processor."
]
},
{
"cell_type": "code",
"execution_count": 7,
"id": "e8af01a9",
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
state
probability
\n",
"\n",
"\n",
"
|0,0,0,0,0,0>
9/25
\n",
"
|{0},0,0,0,0,0>
0.2395
\n",
"
|0,0,{0},0,0,0>
0.2395
\n",
"
|{0},0,{0},0,0,0>
0.1594
\n",
"
|0,0,{0}{4},0,0,0>
4.8193e-4
\n",
"
|{0}{2},0,0,0,0,0>
4.8193e-4
\n",
"
|{0},0,{0}{4},0,0,0>
3.2064e-4
\n",
"
|{0}{2},0,{0},0,0,0>
3.2064e-4
\n",
"
|{0}{2},0,{0}{4},0,0,0>
0
\n",
"\n",
"
"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"pcvl.pdisplay(QPU.source_distribution, precision=1e-4)"
]
},
{
"cell_type": "markdown",
"id": "73af9f32",
"metadata": {},
"source": [
"We can then check the output state distribution corresponding to this input distribution. By default, since our input state had 2 photons, only states having at least 2 detected photons are kept. This can be changed using `min_detected_photons_filter`."
]
},
{
"cell_type": "code",
"execution_count": 8,
"id": "cbee9802",
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
state
probability
\n",
"\n",
"\n",
"
|0,1,0,1>
0.495518
\n",
"
|1,0,1,0>
0.495518
\n",
"
|0,1,1,0>
0.00747
\n",
"
|1,0,0,1>
0.001494
\n",
"\n",
"
"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"output_distribution=QPU.probs()[\"results\"]\n",
"pcvl.pdisplay(output_distribution, max_v=10)"
]
},
{
"cell_type": "markdown",
"id": "3cda6b52",
"metadata": {},
"source": [
"Let us run now the experiment with increasing value of g2 in the range $[0, 0.2]$ with a brightness of $0.15$ and check the CHSH inequality."
]
},
{
"cell_type": "code",
"execution_count": 9,
"id": "3f29137a",
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "30475b1501b14a19ad6caef1e7cb322a",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
" 0%| | 0/40 [00:00"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"plt.title(\"CHSH value with purity\")\n",
"plt.xlabel(\"g2 (%)\")\n",
"plt.ylabel(\"Bell inequality\")\n",
"plt.axhline(y=2, linewidth=2, color=\"red\", label='horizontal-line')\n",
"plt.plot(x, y, color =\"green\")\n",
"plt.grid(color='b', dashes=(3, 2, 1, 2))\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "1329a625",
"metadata": {},
"source": [
"Beyond 13% of g2, we are crossing the value $2$, i.e. not violating anymore the $|CHSH|\\le 2$ inequality!"
]
},
{
"cell_type": "markdown",
"id": "e55db30c",
"metadata": {},
"source": [
"## Reference\n",
"\n",
"> [1] T. C. Ralph, N. K. Langford, T. B. Bell, and A. G. White. Linear optical controlled-NOT gate in the coincidence basis. [Physical Review A](https://link.aps.org/doi/10.1103/PhysRevA.65.062324), 65(6):062324, June 2002. Publisher: American Physical Society."
]
}
],
"metadata": {
"language_info": {
"name": "python"
}
},
"nbformat": 4,
"nbformat_minor": 5
}